Until in the beginning of the years 1990, the paradigm was a universe made up entirely of matter to the critical density. There were some difficulties in particular on the level of the age of oldest stars but uncertainties made it possible to maintain the coherence of the model.
The past decade saw this model called
completely in question. The observations of the great structures posed
the first stakes of the new paradigm. Indeed, the measurements based on
the study of the fluctuations of the distribution of mass of galaxy
cluster showed that the density of matter was low (well below the
canonical value of the time of 1) around ![]() (white1993). To maintain coherence theoretical and in particular to
keep a universe of critical density essential for the models of
inflation, it missed more half of energy. It is as from this time that
the cosmological constant of Einstein started to remake to speak about
it (carroll1992).
(white1993). To maintain coherence theoretical and in particular to
keep a universe of critical density essential for the models of
inflation, it missed more half of energy. It is as from this time that
the cosmological constant of Einstein started to remake to speak about
it (carroll1992).
It had as principal advantage of reconciling measurements of age of stars while making it possible to have universes with a larger age (around 15 billion years), to make it possible to have a critical density in spite of a low density of matter and thus to allow a period of inflation . However, until the middle of the years 1990, the introduction of the cosmological constant was only one pure theoretical suitability allowing the internal coherence of the models. No direct measurement had been able to highlight it.
The first direct
indication of a component in the universe in addition to the black
matter came in 1998 from measurement from distances to supernov├Ž of the
Ia type to redshift of about 0.5 (perlmutter1999 &
riess1998). This measurement provides to the first order a value of ![]() .
It showed that the expansion of the universe was not in deceleration
(as a universe only made up of matter would impose it), but in
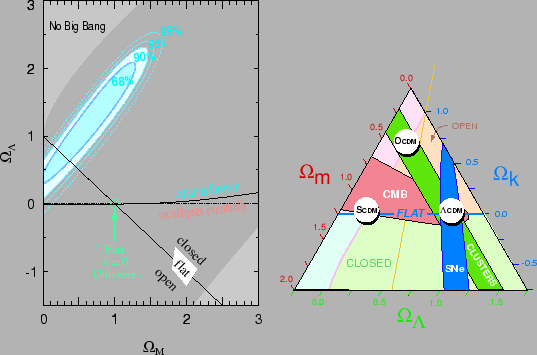
acceleration. The figure of left 1.8 shows the contour of confidence in the plan
.
It showed that the expansion of the universe was not in deceleration
(as a universe only made up of matter would impose it), but in
acceleration. The figure of left 1.8 shows the contour of confidence in the plan ![]() obtained by the Supernova Cosmology Project using 42 supernov├Ž of the
Ia type distant. In particular, the ellipse excludes a universe without
cosmological constant with
obtained by the Supernova Cosmology Project using 42 supernov├Ž of the
Ia type distant. In particular, the ellipse excludes a universe without
cosmological constant with ![]() is around 0.7.
is around 0.7.
Figure 1.8 shows the comparison between the measurements made with the supernov├Ž, the galaxy clusters and the cosmological diffuse bottom. The agreement of three strictly independent measurements made it possible to reinforce the result of measurement of the supernov├Ž.
(spergel2003 & efstathiou2002).
 |
The cosmological constant thus passed in ten years of the statute of constant forgotten to one of the major parameters of modern cosmology.
By using definition 1.20 of ![]() , one can build a density of energy for the cosmological constant:
, one can build a density of energy for the cosmological constant:
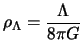 |
(1.31) |
This density does not depend on time. The conservation of energy imposes ![]() .
The cosmological constant can thus be reinterpreted like a fluid of
density constant during time, strictly homogeneous spatially and of
negative pressure.
.
The cosmological constant can thus be reinterpreted like a fluid of
density constant during time, strictly homogeneous spatially and of
negative pressure.
The negative pressure acts like a repulsive gravitation and thus makes it possible to explain the acceleration of the expansion when this one becomes dominant.
The space homogeneity makes it possible to explain why one does not see his influence on the level of the galaxies and the clusters, in particular, at the moment of the formation of the structures.
These characteristics are in any point similar to those of the vacuum (the minimum energy level) of any quantum theory; the description of the acceleration of the universe thus had also a strong impact in the community of the physics of the particles.
An abundance of articles are been published to try to explain the nature of this strange component. This would be a true `` '' constant cosmological, the signature of the energy of the vacuum of the quantum fields, or even a new scalar field of quintessence type or finally the presence of topological defects (cosmic strings, walls of field).
To the moment of its discovery and still today, this new component did not deliver the secrecy of its nature, it carries according to the authors and the assumptions several names: cosmological constant, energy of the vacuum, dark or black energy, quintessence...
In the continuation, we will present this one while following mainly turner2002 and will call it black energy ( ![]() ).
).
To account for the observation, black energy must have the following characteristics: