$\star$ Quintessence

A simple model to describe black energy is to introduce a scalar field with a very slow evolution towards its fundamental state. In an expanding universe, a scalar field of potential $V(\phi)$ with a minimum coupling with gravity obeys the following equation of Klein-Gordon:

$$\ddot \phi + 3 H \dot \phi + V'(\phi) = 0$$ (1.35)

Where $H$ is the growth rate of the universe, the points indicate the derivative compared to time. The growth rate acts like a term of friction, the field is about stationary when $p_\phi = \frac{1}{2 } \dot \phi^2 - V(\phi)$, which implies that its equation of state is written:

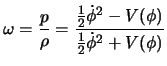$$\omega = \frac{p}{\rho} = \frac{\frac{1}{2} \dot \phi^2 - V(\phi)}{ \frac{1}{2}\dot \phi^2 + V(\phi)}$$ (1.36)

It is seen that the equation of state of this field varies in time. If the variations in the course of time are weak ( $\omega \simeq -1$ and the scalar field has the effective behavior of a cosmological constant (table 1.2 ).

The principal advantages of this type of dynamic model are:

1. It agrees with an energy of the quantum vacuum null, the field of quintessence would simply not have had time to release towards its fundamental.
2. The dynamic nature of the field of quintessence makes it possible to give an explanation to the Nancy-Kerrigan paradox. Indeed, the evolution of the field of quintessence can follow in a more or less parallel way the evolution of the density of matter. However, the value of the density of field depends in a significant way of the parameters on the potential $V(\phi)$.