Contents
The theorists proposed many possibilities to account for black energy:
- A network of topological defects (walls of field, cosmic strings...)
- Scalar fields: quintessence.
- Models of brane and additional size.
- Physics of the axions: coupling of the black matter and black energy.
The simplest way of paramétriser this energy black is its equation of state.
As we saw the universe is homogeneous and isotropic this implies that
the tensor energy impulse must take a form corresponding to a true
fluid:
![$\displaystyle T_X^{\mu \nu} = diag\left[ \rho_{X}, -P_X,-P_X,-P_X\right]$](img189.png) |
(1.33) |
where 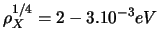 .
.
One can characterize the pressure by his report/ratio with the density of energy:
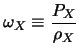 |
(1.34) |
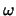 constant. We see that the values most favoured are between -0.7 and -1.
This already seems to exclude the topological models of defects.
constant. We see that the values most favoured are between -0.7 and -1.
This already seems to exclude the topological models of defects.
Table 1.2: Equation of state of black energy according to its nature. In the case of quintessence 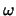 varies dynamically between -1 and 1.
varies dynamically between -1 and 1.
| X |
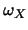 |
Cosmological constant 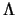 |
-1 |
| cosmic strings |
-1/3 |
| Walls of field |
-2/3 |
| Quintessence |
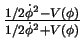 |
|
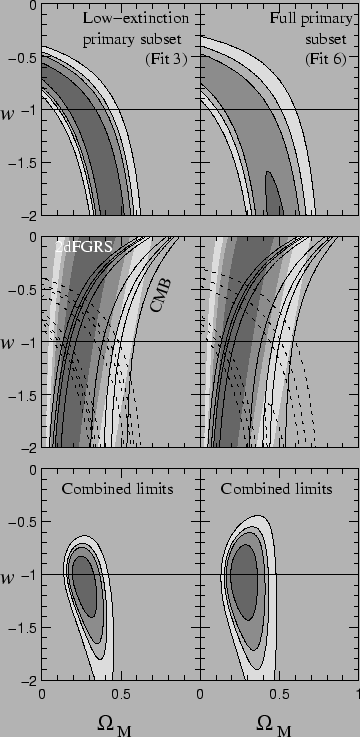
Figure 1.9: Ellipse in the plan 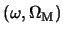 for a flat universe. In top, measurements are presented coming from the
supernovæ. In the medium, are superimposed the ellipses of the
supernovæ, that coming from measurement on the great structures by 2dF
and that coming from the observation from the cosmological diffuse
bottom. In bottom the combined limits of these three measurements are
represented. This figure is drawn from knop2003.
for a flat universe. In top, measurements are presented coming from the
supernovæ. In the medium, are superimposed the ellipses of the
supernovæ, that coming from measurement on the great structures by 2dF
and that coming from the observation from the cosmological diffuse
bottom. In bottom the combined limits of these three measurements are
represented. This figure is drawn from knop2003.
 |
Contents Julien Raux 2004-05-04
![]() .
. 