Contents

Adjustment of PSF

The technique is as follows:

  1. Estimate of the position by weighed barycentre.
  2. Alignment of the PSF on star.
  3. Estimate of flux and the error.

Figure 8.10 indicates to us that the positions are correctly rebuilt with an accuracy of 0.15 pixels on average, which corresponds to a precision of $ 0.007' ' $ .

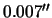Figure 8.9: This figure shows the `` SWEATER '' estimate of fluxes, i.e. the residuals of estimate standardized with their uncertainty. We obtain, Gaussian centered sigma around 1, which indicates that the reconstitution of fluxes is not biased and that the errors are correctly evaluated.
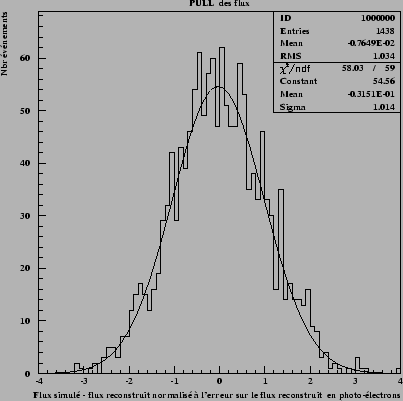\begin{figure}\it\begin{center}\epsfig{file=Images/fakesfluxpull.eps, width=10cm}\end{center}\end{figure}

Figure 8.10: This figure shows the residuals of rebuilding of the positions of stars by estimate of a barycentre weighed by a model of PSF. The residuals are on average null, the dispersion of approximately 0.15 pixels is 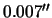$ 0.007' ' $ .
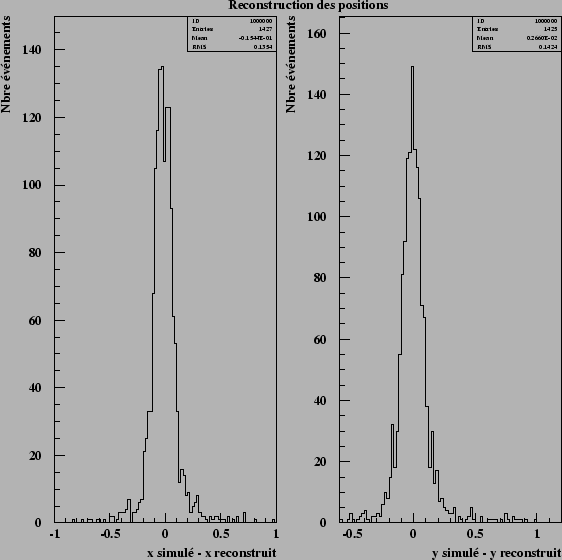\begin{figure}\it\begin{center} \epsfig{file=Images/fakesposition.eps, width=14cm}\end{center}\end{figure}

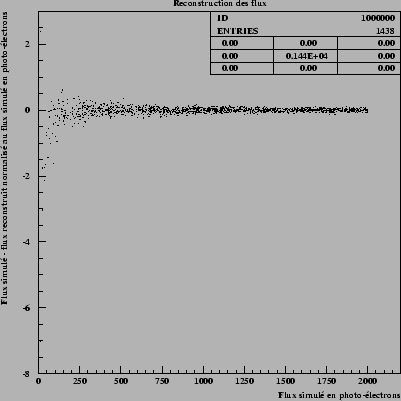
Figure 8.11: This figure shows the residual of the estimate of flux according to simulated flux. It does not appear systematic bias. In particular, the estimate of flux remains not biased with small flux
\begin{figure}\it\begin{center} \epsfig{file=Images/fakesfluxscatter.eps, width=10cm}\end{center}\end{figure}

next up previous contents
suivant: Flux d'ouverture monter: La photométrie avec HuPhot précédent: Simulation et performance de   Table des matières
Julien Raux 2004-05-04