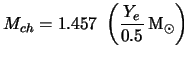Contents
Let us examine the energy balance of dwarf white. Its energy
can be written like a sum of gravitational energy and internal energy.
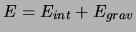 |
(5.11) |
If it is considered that internal energy is
due primarily to the electrons, one can approximate internal energy as
the number of electrons N in the dwarf white one multiplied by the
average energy of these electrons 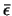 , is:
, is:
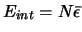 |
(5.12) |
where,
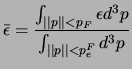 |
(5.13) |
Within the relativistic ultra limit, one finds 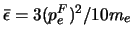 . In these two modes, one obtains respectively for internal energy:
. In these two modes, one obtains respectively for internal energy:
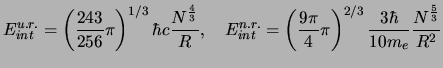 |
(5.14) |
If it is considered that the density of star is uniform, one can write:
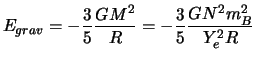 |
(5.15) |
We concentrate on the case ultra-relativist, which becomes relevant during a collapse. We find then for the energy of star:
![$\displaystyle E = \frac{3}{5} \frac{G^2m_B^2}{Y_e^2} \frac{NN_c}{R} \left[\left(\frac{N}{N_c} \right)^{1/3} -\frac{N}{Nc} \right]$](img408.png) |
(5.16) |
with
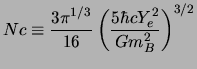 |
(5.17) |
If 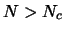 ,
the term between hooks is negative and energy decreases with R, the
electrons are even relativistic. Energy decrease without end when R
tends towards 0, it does not exist minimum.
,
the term between hooks is negative and energy decreases with R, the
electrons are even relativistic. Energy decrease without end when R
tends towards 0, it does not exist minimum.
When 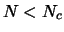 ,
the term between hooks is positive and energy decreases when R
increases, the density decreases then and the electrons become
relativistic. Internal energy decrease then in
,
the term between hooks is positive and energy decreases when R
increases, the density decreases then and the electrons become
relativistic. Internal energy decrease then in 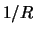 ).
There is thus a ray from which the gravitation will become dominant,
total energy becomes negative and becomes an increasing function of R.
He exists a minimum with E for a finished ray, he thus exists a stable
configuration of dwarf white.
).
There is thus a ray from which the gravitation will become dominant,
total energy becomes negative and becomes an increasing function of R.
He exists a minimum with E for a finished ray, he thus exists a stable
configuration of dwarf white.
Thus, the maximum number of fermions for which a steady balance exists is 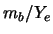 , one finds a mass beyond which mechanical balance is impossible:
, one finds a mass beyond which mechanical balance is impossible:
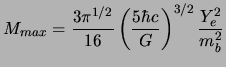 |
(5.18) |
This mass was calculated the first time in 1931 by S.
Chandrasekhar, it is quite naturally that it bears its name. In the
continuation of this talk, we will refer to it as the mass of
Chandrasekhar or more simply 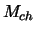 .
.
The numerical application of this calculation, gives us an
over-estimated value of 20%. This error was foreseeable taking into
account in particular the simplified calculation of the average energy
of the electrons.
A carefuller calculation would have given us:
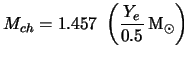 |
(5.19) |
Contents Julien Raux 2004-05-04
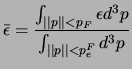
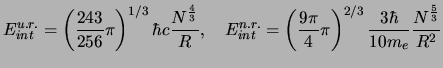
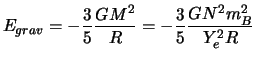
![$\displaystyle E = \frac{3}{5} \frac{G^2m_B^2}{Y_e^2} \frac{NN_c}{R} \left[\left(\frac{N}{N_c} \right)^{1/3} -\frac{N}{Nc} \right]$](img408.png)
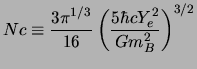
![]() ,
the term between hooks is negative and energy decreases with R, the
electrons are even relativistic. Energy decrease without end when R
tends towards 0, it does not exist minimum.
,
the term between hooks is negative and energy decreases with R, the
electrons are even relativistic. Energy decrease without end when R
tends towards 0, it does not exist minimum. ![]() ,
the term between hooks is positive and energy decreases when R
increases, the density decreases then and the electrons become
relativistic. Internal energy decrease then in
,
the term between hooks is positive and energy decreases when R
increases, the density decreases then and the electrons become
relativistic. Internal energy decrease then in ![]() ).
There is thus a ray from which the gravitation will become dominant,
total energy becomes negative and becomes an increasing function of R.
He exists a minimum with E for a finished ray, he thus exists a stable
configuration of dwarf white.
).
There is thus a ray from which the gravitation will become dominant,
total energy becomes negative and becomes an increasing function of R.
He exists a minimum with E for a finished ray, he thus exists a stable
configuration of dwarf white. ![]() , one finds a mass beyond which mechanical balance is impossible:
, one finds a mass beyond which mechanical balance is impossible: 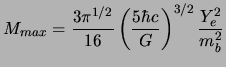
![]() .
.