We know now that the essence of the physics of dwarf white rests on balance between the pressure of Fermi of the electrons and the gravitation. We now will see which are the equations which govern this ultra-dense and degenerated matter.
To start, let us see the characteristics of such a star. If one considers dwarf white of ![]() .
.
The temperature of Fermi of the electrons is given by:
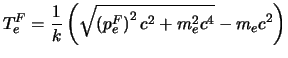 |
(5.5) |
| (5.6) |
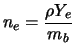 |
(5.7) |
The pressure of a degenerated gas of electrons is given by diu1989 (Complement VI B p860):
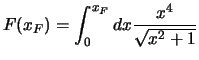 |
(5.9) |
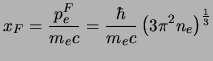 |
(5.10) |
We saw that the gas of electrons is degenerated, and thus that its
energy is independent of the temperature. Thus it is pressure of the
electrons which is the pressure of star. One can regard equation 5.8 besides as the equation of state of star (in substituent the density in ![]() ),
and one sees that the temperature does not intervene there. The
temperature of star is however not unspecified: the nuclear matter
fixes it according to the density and pressure (electrons).
),
and one sees that the temperature does not intervene there. The
temperature of star is however not unspecified: the nuclear matter
fixes it according to the density and pressure (electrons).
We now will study the mechanical stability of this gas of degenerated electrons.