The K-correction

The photometric observation of the astronomical sources, whose spectrum can have significant variations, is carried out by using instruments with a certain band-width .

In particular, measured flux represents only one fraction of the spectrum of the object considered. The redshift of the spectrum due to the cosmological recession thus involves that the part of the spectrum observed in a given band-width evolves/moves.

The measurement of the distances rests on a comparison of flux of standard candle, one thus needs all the observations in the same photometric reference frame, a given band-width, to be able to make coherent measurements of distances.

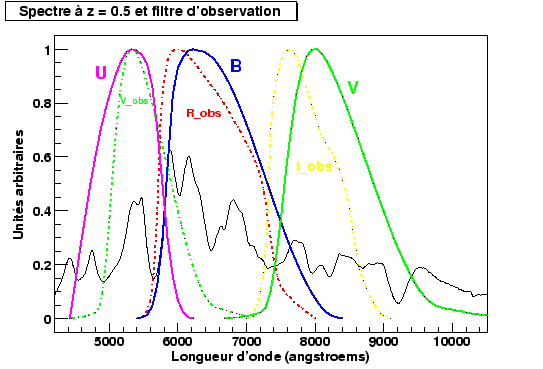
Figure 2.4 shows for the supernovæ of the type Ia, the effect of the shift towards the red on the zone covered by the various filters considered.

Figure 2.4: Correction for a supernova of the Ia type to a redshift of 0.5. This figure shows that for this kind of spectral shift, the red band of observation (R) corresponds to the blue part of the spectrum of the supernova in its reference frame. To measure flux in the blue part of the spectrum, one must thus observe the supernova in the red filter.

Let us consider an object whose spectrum is $T_{restframe}(\lambda)$ (in which one supposes that the object behaves like a standard candle) is considered in the reference frame of the object. For the moment, we consider that emitted flux is constant in time.

Flux in the reference frame of the object in the filter of reference is written:

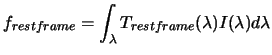$$f_{restframe} = \int_\lambda T_{restframe}(\lambda) I(\lambda) d\lambda$$ (2.22)

The flux observed of the spectrum shifted towards the red (the factor $(1+z)$ in the following equation) is written him:

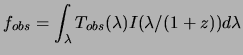$$f_{obs} = \int_\lambda T_{obs}(\lambda) I(\lambda/(1+z)) d\lambda$$ (2.23)

The report/ratio of these two fluxes gives the term by which it is necessary to multiply flux actually observed to bring back itself in the filter of reference. In practice, these corrections are made by using the system magnitudes; it is pointed out that in a filter given the magnitude is written:

$$m_{filtre} = -2.5\log_{10}(f_(filtre)/f_0(filtre))$$ (2.24)

where $I_0$ the spectrum of star of reference.

One can thus write the K-correction like the difference the magnitudes observed of our object in the two reference frames:

$$K(z) = m_{obs} - m_{restframe }$$ (2.25)

and thus:

$$K(z) = -2.5\log_{10}\left(\frac{\int_\lambda I(\lambda) T_{obs} d... ...}\left( \frac{\int_\lambda I_0 T_{obs}(\lambda)}{\int I_0 T_{restframe}}\right)$$ (2.26)

If one makes moreover the assumption that the flux of the object evolves/moves in the course of time, the flux emitted during an interval of time $-2.5\log_{10}(1+z)$ to the expression of the K-correction.

Lastly, in case simple where the observant filters and in the reference frame of the object are the same ones (what will be generally the case for the observations with weak spectral shifts), the correction of error K becomes independent of star of reference.

To finish, the correction is in practice difficult to set up, it requires in particular to have a good knowledge of the spectrum of the object studied . In practice, the spectra used are built starting from a compilation of the spectra observed for the same type of objects.

Moreover, for the great redshifts, the corrections are inter filters, it is then necessary to utilize the spectrum of star of reference and to have a good knowledge of the instrumental filters to allow a not-biased correction.

Lastly, to reduce the importance of this correction, it will be necessary to choose the filter used for the observations nearest to the filter of reference. A possibility is to build the filters corresponding to the usual band-widths shifted towards the red to correspond to that of the object observed, which makes it possible in practice to minimize the corrections. This method applied by schmidt1998 is in practice difficult to put in uvre, it requires in particular to have filters for all the ranges of spectral shifts. Moreover, for certain space telescope and observation aids in particular Hubble, it is impossible to change the filters of observations. The practice is thus to choose the standard filter which is closest to the filter considered in the reference frame of the supernova.