Return on black energy

As we have it in the preceding chapter, a true `` '' constant cosmological is only one model among other to explain the acceleration of the expansion. While beginning again, the equation of state 1.35 , one can récrire the distance from luminosity like:

$$d_L = (1+z) \frac{c}{H_0\vert\Omega_{\rm k_0}\vert^{1/2}} {\cal S... ...\rm M_0}(1+z')^3 +\Omega_{\Lambda_0}(1+z')^{3(1+\omega_X)}\right]^{1/2}}\right)$$ (2.12)

If moreover, one makes the assumption that the function of state of black energy is variable in time or in an equivalent way with the redshift, it becomes:

$$P_X = \omega_X(z) \rho_X$$ (2.13)

The conservation of energy makes it possible to determine the evolution of the density of black energy:

$$d(\rho_Xa^3) = -\omega_X(z) \rho_X d(a^3)$$ (2.14)

thus:

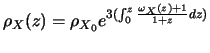$$\rho_X(z) = \rho_{X_0} e^{3(\int_0^z \frac{\omega_X(z)+1}{1+z}dz)}$$ (2.15)

And finally, one can récrire the distance from luminosity like:

$$d_L = (1+z) \frac{c}{H_0\vert\Omega_{\rm k_0}\vert^{1/2}} {\cal S... ...\int_0 ^{z'} \frac{1+\omega_X(z'')} {1+z''} dz''\right) } \right]^{1/2}}\right)$$ (2.16)

In theory, it is thus possible to measure the dependence of $\omega_X$ according to the redshift by measuring distances from luminosity. As we saw in the first chapter, this measurement is extremely difficult and is not, in the state current of the observations, not realizable. However, as astier2000 and goliath2001 show it, future satellite SNAP will be able to estimate the variations of $\omega_X$ according to the redshift. In particular, it is discussed the precision which could be reached, by measuring the distance from 2000 supernovæ, to the measures of first derived from $\omega_X(z)$.