The distance from luminosity

If an intrinsic object of luminosity is considered $\cal L$ whose radiation is isotropic, this radiation uniformly will then be distributed on a sphere. In the metric one of Robertson-Walker, the element of surface is written: $t=t_0$, one, expressed in the frame of reference comobiles:

$$S = 4 \pi R^2_0 {\cal S}^2_k(\chi)$$ (2.5)

So now, we consider a telescope whose mirror has a surface $\delta t_0 = \delta t_1 \frac{a(t_0)}{a(t_1)}$. The power received by the mirror is thus written like the report/ratio of surfaces, multiplied by the intrinsic luminosity of the object, multiplied by $\left(\frac{a(t_0)}{a(t_1)}\right)^2$ :

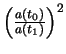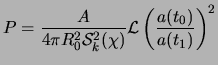$$P = \frac{A}{4\pi R_0^2 {\cal S}^2_k(\chi)} {\cal L} \left(\frac{a(t_0)}{a(t_1)}\right)^2$$ (2.6)

By definition, the apparent luminosity or flux is the power received per unit of area: $1+ Z = \frac{a(t_0)}{a(t_1) }$ :

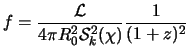$$f = \frac{{\cal L}}{4\pi R_0^2 {\cal S}^2_k(\chi)} \frac{1}{(1+z)^2}$$ (2.7)

The distance from luminosity is defined like:

$$d_L^2 \equiv \frac{{\cal L}} {4\pi f} = R^2_0 {\cal S}_k^2(\chi) (1+z)^2$$ (2.8)

And thus,

$$d_L = R_0 {\cal S}_k(\chi) (1+z)$$ (2.9)

While using, equation 1.20 ), it comes:

$$d_L(z) = \frac{c (1+z)}{H_0\sqrt{\vert\Omega_{\rm k_0}\vert}} {\c... ...[(1+z')^2(1+\Omega_{\rm M_0}z') -\Omega_{\Lambda_0}z'(2+z')]^{-1/2} dz' \right)$$ (2.10)

For redshifts small, one can rewrite this relation:

$$d_L = \underbrace{\frac{cz}{H_0}\left(1 + \frac{1-q_0}{2} z + {\cal O}(z^2) \right) }_{{\rm pour\ } z \ll 1}$$ (2.11)

The measurement of the flux $f$ of an object which one knows the intrinsic luminosity ( a standard candle ) thus allows a direct measurement of the distance, and thus to force the cosmological parameters.

Moreover, equation 2.11 shows that the measurement of distance from objects whose shift towards the red is small in front of 1 allows the measurement of the constant of Hubble the first order and of the parameter of deceleration the second order.

It is mainly this type of measurement which was carried out for the measurement of the constant of Hubble that we presented in the preceding chapter. By using the measurement of distance from objects in the flood of Hubble (for shifts towards the red around 0.05).

The same method was applied for the determination of the cosmological parameters by using the supernovæ like standard candles to redshifts around 0.5.

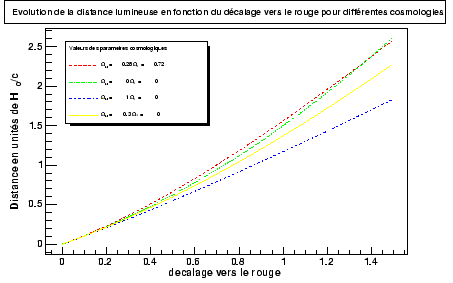
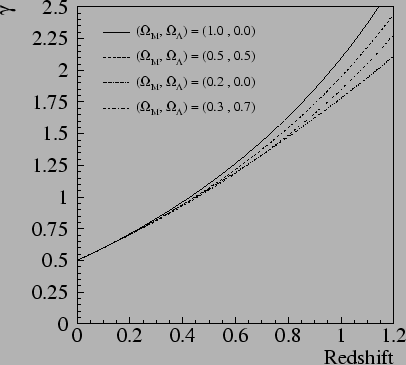
The ambition of this thesis is to use this same method for supernovæ with redshifts more significant (typically 1). Indeed, as figure 2.1 shows it , the various models (correspondent with various sets of cosmological parameters) see their variations increasing with the shift towards the red.

Figure 2.1: Outdistance luminosity according to the redshift for 4 models of different universes. A universe empties ( $\Omega_\Lambda = 0.72$). It will be noticed that the degeneration between the various models starts to be raised for redshifts around 0.5.

With each value of redshift, to measure a distance from luminosity (only one quantity) constrained a linear combination of the cosmological parameters which one wishes to estimate. For the case ( $\gamma=1$ for which the measured combination is orthogonal with the curve is very close to z=0.5 for the scenarios considered.

Appear: Tangent of the angle of degeneration ( $\Omega _ \Lambda$) like function of the redshift for 4 models of different universes. There paramétrise the measured combination is a shift given like $2\Omega_{\rm M}-\Omega_\Lambda$ with z=1. That illustrates incidentally that the influence of the cosmological constant decrease when Z believes.

We will see in continuation 6 that measurements with very great redshift also make it possible to better include/understand the systematic errors.