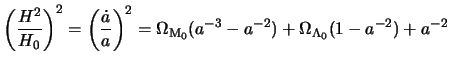The model of current universe and measurements of distance

As we saw, the dynamic evolution of the universe corresponds to its energy content. The most recent observations taught us that the universe is primarily composed of two types of fluids. First is in black matter shape the nonrelativistic. The second has a nature for the moment still unknown; he has a behavior similar to the cosmological constant. Let us see which are in this paradigm the solutions of the equations of Friedmann-Lemaître.

By considering only these two fluids, the equation of Friedmann 1.23 can be rewritten in the form:

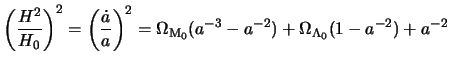$$\left( \frac{H^2}{H_0} \right)^2 = \left( \frac{\dot a}{a} \right)^2 = \Omega_{\rm M_0} (a^{-3} -a^{-2}) + \Omega_{\Lambda_0}(1 -a^{-2}) + a^{-2}$$ (2.1)

The light follows the geodetic ones of the universe, one can thus write the co-ordinate comobile $\chi$ between two points like:

$$\chi = \int_{t_0}^{t}\frac{dt}{R(t)}$$ (2.2)

One deduces the value from it from the distance comobile according to $\chi(z) = 1/R_0 \int_1^{a(z) } da/a\dot a$, then redshift and of the cosmological parameters:

$$\chi(z) = \sqrt{\vert\Omega_{k_0}\vert} \int_0^z[(1+z')^2(1+\Omega_{\rm M_0}z') -\Omega_{\Lambda_0}z'(2+z')]^{-1/2} dz'$$ (2.3)

This expression is at the base of all the estimates of the geometrical cosmological parameters.