$\star$ Nonbaryon matter

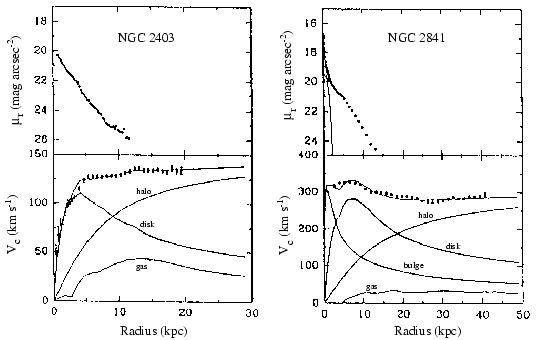
Measurements of density of matter by gravitational effects showed that it `` missed '' almost 90% of the matter to account for the dynamics of all the structures whose size is higher than the globular clusters. In particular, the curves of rotation of the galaxies (see figure .

Figure 1.6: Curve of rotation of spiral galaxies NGC2403 and NGC2841. The higher part gives the variation of the brightness of surface $V_c(r)$ are represented in bottom, are superimposed on the best adjustment of a galactic model including/understanding a bulb, a disc, gas and a spherical halation of dark, essential matter to account for the plate observed beyond $10\, \mathrm{kpc}$ (according to [ BegemanBegeman1987 ]).

Moreover, the observation of the gravitational effects of the great structures indicates that the mass of these objects is nearly 1 order of magnitude higher than the sum of all the baryon components than they contain.

Lastly, the galaxies and the galaxy clusters were formed by gravitational matter not-relativist collapse. It is difficult to include/understand how, starting from an almost homogeneous baryon distribution at the time of decoupling matter-radiation (as indicates it measurements of the CMB), of the inhomogeneousness could grow to allow to produce the distributions of galaxies and cluster currently observed.

Figure 1.7: Simulation Virgo (thomas1998 & jenkins1998) of the evolution of the great structures according to the shift for 4 configurations different of universe from top to bottom: the model `` standard '' $H_0 = 70\rm \, km\:s^{-1}\, Mpc^{-1}$.

The current models (in particular the model Cold Dark Matter CDM, peebles1982 for the theoretical introduction, davis1985 for the first simulations) suppose that there is massive black matter interacting only by weak interaction . It would have been uncoupled from the matter and of the electromagnetic radiation when the universe had a temperature of the order of MeV. It could correspond to the lightest particles of the models of supersymmetry which associate the traditional elementary particles (quarks, leptons, bosons of gauge and Higgs) of the partners by a symmetry fermions/bosons. This symmetry cannot be exact, because these hypothetical partners would have the same mass then as the particles that we know, and would have being observed in great number, in particular with the LEP. Lightest of these supersymmetric partners `` '' is in theory stable and could be present in the form of a diffuse bottom of particles at the manner of the CMB or bottom of neutrinos.

Many experiments so much of physics on accelerator (FermiLab or the future LHC), that of astroparticules (ELDELWEISS or CDMS Abusaidi2000) try to highlight this new matter shape. The most favorable models of supersymmetry make it possible to hope that these particles could be observed within 10 years.

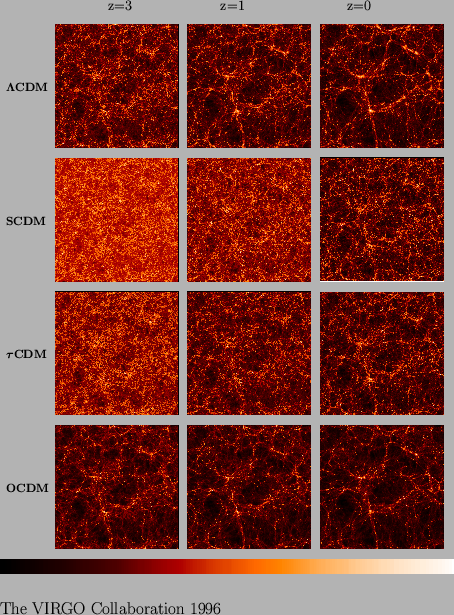
From a point of view of cosmology, model CDM and its refinements including the cosmological constant are the only ones with being able to account for the formation of the structures (Cluster and Galaxies) in a realistic way. Indeed, the digital simulations like that carried out by thomas1998 and jenkins1998 show that only these models make it possible to reproduce the structures observed. These simulations are presented in figure 1.7 .

The transition from a universe dominated by the radiation to a universe dominated by the matter depends on $\Omega_M$. This transition has a signature in the current spectrum of fluctuations of density on a large scale. The data coming from the surveys of galaxies 2dF (efstathiou2002) and SLOAN DIGITAL Sky Survey (dodelson2002) give respectively:

$$\Omega_M h= 0.23 \pm 0.09$$ (1.29)

$$\Omega_M h= 0.20 _{-0.09}^{+0.16}$$ (1.30)