Geometry of the universe

The radiation of the cosmological diffuse bottom was emitted meadows of $300\, 000$ years after the Big-bang corresponds to the period when the temperature became sufficiently low to make it possible the electrons to combine with the protons to form the first atoms, then first molecules (in the very great majority of hydrogen and helium). Previously, the universe formed a plasma which was completely opaque with the radiation. The universe thus became at that time transparency. The photons produced at the time of the recombination thus could travel being observed since then today. The fossil cosmological radiation represents a cosmological mine of information. In particular, we will show in the continuation how it could be used to force the cosmological parameters and in particular the geometry of the universe.

The CMB has anisotropies; they correspond to relative variations of temperature about $10^{-5}$. One can show that these variations are directly connected to the fluctuations of density at the time of the recombination.

It is the study of the variations of density which will make it possible to force cosmology.

Indeed, the fluctuations of density allow the collapse of the matter and the radiation in the formed wells of gravitational potentials, which involves an increase in temperature. Thus, a photon coming from a on-dense area will be hotter, while a photon coming from a less dense area will be colder.

In addition, the heating of gas increases the pressure of radiation of the photons and can cause a stop of the collapse followed by a dilation. There is appearance of oscillations.

These oscillations can be interpreted like acoustic waves. The greatest scale reached by these waves is the horizon of these sound waves which move at a speed $c_s = c/3$. The greatest amplitudes in the oscillations are thus a direct measurement of the size of the horizon at the time of the recombination.

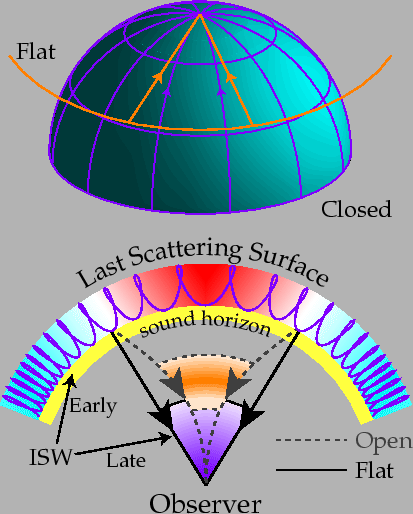
As figure 1.4 shows it , the measurement of the angular size of an object which one knows dimension makes it possible to make a measurement of the geometry of the universe.

Figure 1.4: These two figures illustrate how the measurement of the angular size of the oscillations of the cosmological bottom allows a measurement of the geometry of the universe. The angular size observed of the object considered (here the horizon of the acoustic waves produced by the fluctuations of densities) depends directly on the geometry.

The measurement of the fluctuations of temperature thus allows a direct measurement of the geometry. In practice, the amplitude of the fluctuations is given according to their angular scale on the sky. For that, one breaks up them on a basis of spherical harmonics:

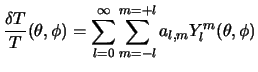$$\frac{\delta T}{T}(\theta,\phi) = \sum_{l=0}^{\infty} \sum_{m=-l}^{m=+l}a_{l,m}Y_l^m(\theta, \phi)$$ (1.23)

Each multipolar moment $c_l = \frac{1}{2l+1}\sum_{m=-l}^{+l } \vert a_{lm}\vert^2$ which measure the importance of these fluctuations on a corresponding angular scale.

In this representation, one can show that the first peak corresponds to the greatest amplitudes of temperature and thus of density (which corresponds to the horizon of the acoustic waves at the time of the recombination). The measure of location of this peak thus allows an estimate of the angular size of these fluctuations and thus of the geometry. The result of WMAP is (spergel2003):

$$1-\Omega_{\rm k}= 1.02 \pm 0.02$$ (1.24)

Figure 1.5 exit of spergel2003 shows the measurement made by satellite WMAP. It in particular made it possible to refine measurements of several embarked experiments in balloon stratospheric (Boomerang and MAXIMUM, jaffe2001 or Archeops, Benoit2003), while measuring $1-\Omega_{\rm k}$ with a very high degree of accuracy, it made it possible to show that the universe was almost flat.

Figure 1.5: Spectrum of power obtained with the data resulting from the first year of observation from the cosmological diffuse bottom by satellite WMAP. It brings in particular the most precise measurement of the position of the first peak and thus the strongest constraint on the geometry of the universe (cf text).

We will see in the continuation that the study of the other peaks of the spectrum of $c_l$ allows the measurement of other cosmological parameters.