Contents
The general form of the equation of Friedmann can be rewritten while posing 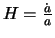 :
:
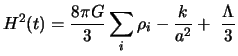 |
(1.14) |
By dividing the two members by 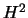 , one obtains:
, one obtains:
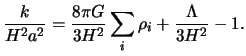 |
(1.15) |
As the first member is sign of K, whatever the T, it is thus second. One can pose:
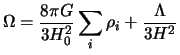 |
(1.16) |
who defines a critical density without dimension, dependent on time.
This one separates the on-dense universes from the under-dense
universes and corresponds to a universe spatially flat (k=0). In the
cosmological absence of constant, the value of 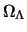 as being the reports/ratios of the terms of the member of right-hand
side of the equation of Friedmann and the square of the growth rate:
as being the reports/ratios of the terms of the member of right-hand
side of the equation of Friedmann and the square of the growth rate:
One can thus rewrite the equation of Friedmann-Lemaître in the extremely simplified form:
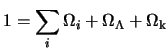 |
(1.20) |
or in an equivalent way:
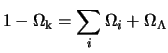 |
(1.21) |
The sum of the energy components of the
member of right-hand side makes it possible to measure the geometry of
the universe directly. It will be noticed that this relation is true
whatever 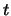 . The equation of state, i.e. ,
the relation which binds the density of these fluids to their pressure,
of the three types of fluids introduced previously, makes it possible
to describe the dynamic evolution their densities. It is the knowledge
of the equations of state of each fluid present in the equation of
Friedmann which will make it possible to solve it.
. The equation of state, i.e. ,
the relation which binds the density of these fluids to their pressure,
of the three types of fluids introduced previously, makes it possible
to describe the dynamic evolution their densities. It is the knowledge
of the equations of state of each fluid present in the equation of
Friedmann which will make it possible to solve it. Figure 1.3
shows the typical evolution of these densities according to the scale
factor. Typical evolutions of the three fluids: matter, radiation and
cosmological constant are respectively proportional to 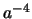 and constant (weinberg1972, chapter 15).
and constant (weinberg1972, chapter 15).
By combining these relationships to the equation 1.14 , one can reexpress the value of the growth rate according to the current values of the cosmological parameters:
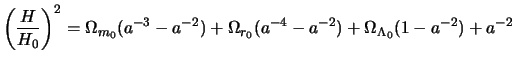 |
(1.22) |
where 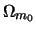 are respectively the current values of the reduced densities for the
components of the radiation type (relativistic) and matter (not
relativist). This equation makes it possible to see the influence of
the various parameters. The matter and the radiation tend to slow down
the expansion. On the other hand, the term corresponding to the
cosmological constant tends to accelerate the expansion.
are respectively the current values of the reduced densities for the
components of the radiation type (relativistic) and matter (not
relativist). This equation makes it possible to see the influence of
the various parameters. The matter and the radiation tend to slow down
the expansion. On the other hand, the term corresponding to the
cosmological constant tends to accelerate the expansion.
Contents Julien Raux 2004-05-04
![]() :
: ![]() , one obtains:
, one obtains: 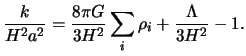
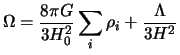
![]() as being the reports/ratios of the terms of the member of right-hand
side of the equation of Friedmann and the square of the growth rate:
as being the reports/ratios of the terms of the member of right-hand
side of the equation of Friedmann and the square of the growth rate: 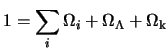
![]() and constant (weinberg1972, chapter 15).
and constant (weinberg1972, chapter 15).