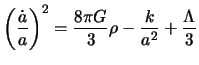 |
 |  | (1.11) |
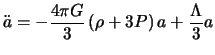 |
 |  | (1.12) |
The equations of Einstein for the metric one of Robertson-Walker and the tensor energy impulse of a true fluid are simplified to give the equations which were derived for the first time indépendemment by Friedmann, then by lemaitre1931. From their highly symmetrical nature, only two noncommonplace equations can be written:
The first equation (which one calls equation of Friedmann)
measurement evolution of the growth rate of the universe according to
time. The value of this rate at our time is the constant of Hubble (![]() ).
).
The second equation gives the value of the acceleration of the expansion. One can define the parameter of deceleration without dimension
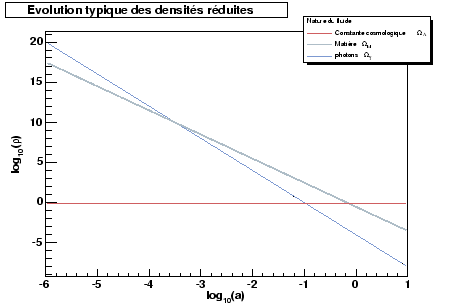 |