$\star$ The expansion

As we saw, combination of the equations of Einstein and the pleasing cosmological principle in a completely natural way the concept of universe dynamic.

In the notations introduced previously, the growth rate is written:

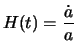$$H(t) = \frac{\dot a }{a}$$ (1.8)

Where the point indicates the derivative compared to time.

It is Slipher and Hubble which, for the first time in 1926, showed that the universe was expanding (hubble1931) thanks to the observation of spectra of galaxies with the telescope of the Wilson mount.

E Hubble noticed that the spectra of the galaxies were all the more shifted towards the red which them luminosity was weak. It deduced from it the law which bears its name which connects the speed $D_{gal}$):

$$v_{gal} = D_{gal} H_0$$ (1.9)

where the constant of proportionality $H_0$ rest on the same principle: measurement specifies distance from objects which one measures the speed of recession thanks to their shift towards the red.

Measurements are difficult because the close objects (some Mpc ) have particular speeds (their own movement made abstraction of the expansion) of the same order of magnitude as their cosmological recession. To abstract itself from this difficulty, one chooses sufficiently distant objects to be able to neglect their own movement and sufficiently brilliances to allow their observation.

One of the principal scientific objectives of the space telescope Hubble is, through the HST Key Project (freedman2001), measurement the constant of Hubble using primary measurement of distance (by using the relation period-luminosity of stars of the céphéides type present in the close galaxies) making it possible to gauge estimators of secondary distance. These methods allow, by using very luminous objects (galaxies or supernovæ) to reach the flood of Hubble where the own movements of the objects become negligible in front of the movement of cosmological recession of origin. The results as well as the various methods employed are described in table 1.1 .

Table 1.1: Results of measurements of the constant of Hubble by the HST Key Project (freedman2001).
The relation of Tully-Fischer connects the number of revolutions of the spiral galaxies and their luminosity.
The Faber-Jackson method or fundamental plan connects the dispersion speeds of the elliptic galaxies to their luminosity. Measurements of brightness of surface use the measurement of the local fluctuation of surface of the galaxies on a fixed angular sector.
The supernovæ of the Ia type are used as standard candles.
The method of photosphere expanding connects the temperature of the supernovæ of the type II, the speed of expansion of its layers and its lightcurve to deduce its angular distance from it.

Methods	Measure of
Tully-Fischer	$71 \pm 3 \pm 7$
Fundamental plan (Faber-Jackson)	$82 \pm 6 \pm 9$
Fluctuation of brightness of surface	$70 \pm 5 \pm 6$
Supernovas of the Ia type	$71 \pm 2 \pm 6$
Supernovas of the type II	$72 \pm 9 \pm 7$

Measurements are followed of their statistical error, then of their systematic error.

Other methods as the measurement of the Sunayev-Zeldovitch effect or by the effects of gravitational lens made it possible to give independent results compatible with the values using the céphéides. They remain however less precise.

Even if there remain dissensions, in particular to the measures implying of the supernovæ of the Ia type apart from the HST Key Project which seems to give lower values, various measurements $70 \pm 5 \rm \, km\, s^{-1}\rm \, Mpc^{-1}$ krauss2002.