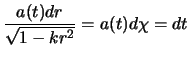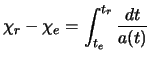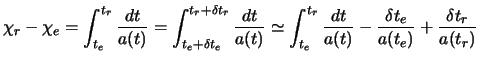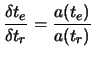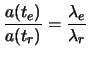$\star$ The shift towards the cosmological red

Let us see how it can be interpreted within the cosmological framework: we study for that the trajectory of a photon in the metric one of Robertson-Walker.

The distance covered by a luminous ray by a motionless source emitted at time 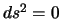$ds^2 = 0$, that is to say in the metric one of Robertson-Walker:

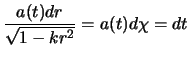$$\frac{a(t)dr}{\sqrt{1-kr^2}} = a(t) d\chi = dt$$ (1.5)

While integrating, it comes:

$$\chi_r -\chi_e = \int_{t_e}^{t_r}{\frac{dt}{a(t)}}$$

By rewriting this equality:

$$\chi_r -\chi_e = \int_{t_e}^{t_r}\frac{dt}{a(t)} = \int_{t_e+\del... ...}^{t_r}\frac{dt}{a(t)} - \frac{\delta t_e}{a(t_e)} + \frac{\delta t_r}{a(t_r)}$$

We have:

$$\frac{\delta t_e}{\delta t_r} = \frac{a(t_e)}{a(t_r)}$$

While reintroducing the wavelengths of these luminous rays which undergo the same redshift ( 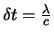$\delta T = \frac{\lambda}{c}$), it comes:

$$\frac{a(t_e)}{a(t_r)} = \frac{\lambda_e}{\lambda_r}$$

As follows:

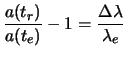$$\frac{a(t_r)}{a(t_e)}-1 = \frac{\Delta \lambda}{\lambda_e}$$ (1.6)

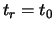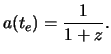Who is the introduced definition of the redshift equation 1.4 . One chooses $t_r=t_0$:

$$a(t_e) = \frac{1}{1+z}.$$ (1.7)

This relation makes it possible to directly connect the redshift observed the scale factor at the time of emission.