Contents

Corrections of filters and filters standard

As we saw photometry depends on the filter in which the observations are made. Flux observed depends indeed on the spectral width of the filter and its evolution according to the wavelength.

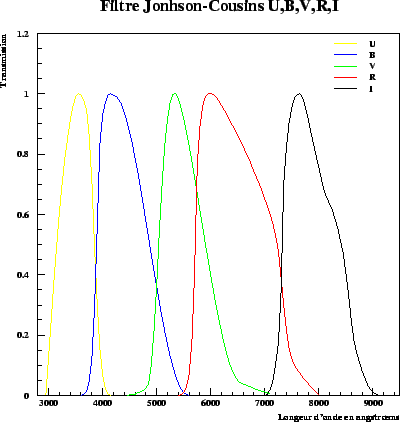
In theory, the built-in filters on the instruments of observation are built to be close to standard filters UBVRI defined by Jonhson (johnson1951, johnson1953) and Cousins (cousins1976). The A.1 figure shows the band-widths of these filters.

Appear A.1: Filter standard UBV Johnson and IH Cousins johnson1951, johnson1953 & cousins1976 standardized with the unit.
\begin{figure}\it\begin{center} \epsfig{file=Images/Filtre_Johnson_Cousins.eps, width=10cm}\end{center}\end{figure}

Appear A.2: Filters UBVRI of Bessel (bessel1990 & bessel1995) standardized with the unit.
\begin{figure}\it\begin{center} \epsfig{file=Images/Filtre_Bessel.eps, width=10cm}\end{center}\end{figure}

Appear A.3: Effective filters of camera CFH12K assembled on the CFHT standardized to reproduce items zero of the instrument.
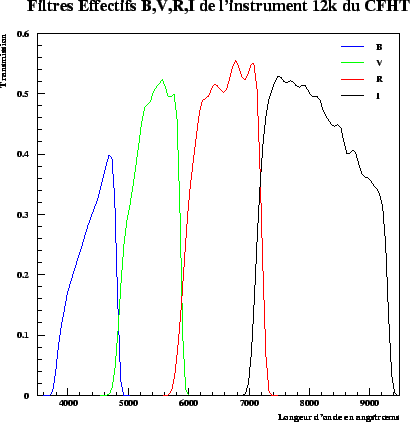\begin{figure}\it\begin{center}\epsfig{file=Images/Filtre_Effectif_12k.eps, width=10cm}\end{center}\end{figure}

However, as the figures A.3 and it , the band-widths of the systems of observation constitute only one approximation of the standard filters. The magnitudes of stars corrected for atmospheric absorption can present variations of the order of the hundredth magnitude, even of the tenth from one instrument to another.

This difference is all the more large as the color of the object considered, i.e. , the difference between the magnitudes observed in two different filters

The bias introduced by the inadequacy between the observational filter and the standard filter is thus at first approximation proportional to the color, to eliminate this bias, corrections of colors or corrections of filters are applied .

They can be written by using the colors of the sources considered:

$\displaystyle m_{corr} = m + \alpha_c (X-Y) + \beta_c(X-Y)^2 + \dots$ (A.19)

where $ \beta_ are the colour terms to the first and the second order of the filter considered. In general, the first order terms are sufficient to correct the magnitudes. The Hubble telescope of share its space position has instrumental filters very different from the land force filters, the transformations of the filter corrections of second order are thus in general applied (holtzman199รค).

Contents
Julien Raux 2004-05-04