Corrections of airmass

The atmospheric extinction is in the broad sense, the reduction of the intensity of a source of radiation resulting from absorption and the diffusion by the atmosphere. The two processes attenuate flux coming from a given source (approximately 1/6 for a source with normal incidence in the filter V).

A vertical luminous ray undergoes between altitudes $dL$ :

$$dL(\lambda,h) = \kappa(\lambda,h)\rho(h) L(\lambda,h) dh$$ (A.8)

where $\rho(h)$ is the density of the air according to altitude.

While integrating A.8 , it comes:

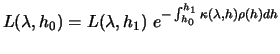$$L(\lambda, h_0) = L(\lambda,h_1)~e^{-\int_{h_0}^{h_1}\kappa(\lambda, h)\rho(h)dh}$$ (A.9)

where $\kappa$ is constant through the atmosphere, one obtains:

$$L(\lambda, h_0) = L(\lambda, h_1) e^{-\kappa(\lambda)\int_{h_0}^{h_1}\frac{\rho(h)}{\cos z} dh}$$ (A.10)

The integral in A.10 represents the airmass contained in the column parallel with the incidental ray. It is not the definition of the airmass generally met in astronomy. This one is defined as the number thickness of atmosphere to the zenith along the line of sight is the number $X$ without dimension:

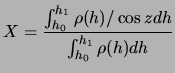$$X = \frac{\int_{h_0}^{h_1}\rho(h)/\cos z dh} {\int_{h_0}^{h_1}\rho(h)dh}$$ (A.11)

While using the definition of the airmass and while introducing $h_0$, it comes:

$$L(\lambda, h_0) = L(\lambda,h_1) e^{\kappa(\lambda) \alpha X(z)}$$ (A.12)

And thus in magnitude:

$$m(\lambda,h_0) = m(\lambda,h_1) +2.5\log_{10}(e) X(z) \alpha \kappa(\lambda)$$ (A.13)

that is to say:

$$m(\lambda,h_0) = m(\lambda,h_1) +k(\lambda) X(z) \alpha$$ (A.14)

known under the name of law of Bouguer , with:

$$k(\lambda) = 2.5\log_{10}(e)\kappa(\lambda)\alpha \simeq 1.086 \kappa(\lambda)\alpha$$ (A.15)

who is the coefficient of extinction.

In the usual filters of observation, measurements are more affected in blue than in the red. The made observations with great zenith angle are reddened.

If one considers a filter of observation of transmission $I(\lambda)$ we let us can write flux like:

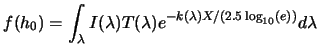$$f(h_0) = \int_{\lambda} I(\lambda) T(\lambda) e^{-k(\lambda)X/(2.5\log_{10}(e))} d\lambda$$ (A.16)

If it is considered, with the first order that the atmospheric extinction is constant in the filter of observation, one can write:

$$f(h_0) = e^{-k(\lambda_0)X/(2.5\log_{10}(e))} \int_{\lambda} I(\lambda) T(\lambda) d\lambda$$ (A.17)

where $h=h_1$) and flux of observation, are written in magnitude:

$$\Delta m = m(h_1) - m(h_0) = -k_0 X$$ (A.18)

where $k_0$ is the principal coefficient of extinction.

In any rigour, atmospheric absorption is not constant according to the wavelength, a more precise analysis makes it possible to determine the corrections of a higher nature (see sterken1992 chapter 6).

However, in practice, if the observations are made with reasonable masses of air (less than 1.5), the term of first order makes it possible to obtain errors around 0.01 magnitude, the same order of magnitude as the typical precise details obtained for zero points.