The metric one of Robertson-Walker

The isotropy and the homogeneity of the universe were postulated in the form of the `` cosmological principle '' by Einstein, then by Friedmann and Lemaître. They were introduced on primarily philosophical bases (the ground does not occupy a place privileged in the universe). The recent observations came to give a justification a posteriori .

One can thus consider with a good approximation which the universe is maximalement symmetrical. One can show (weinberg1972, chapter 13) that for this type of geometry, the metric one is written in polar co-ordinates:

$$ds^2 = dt^2 - R^2(t) \left[ \frac{dr^2}{1-kr^2} + r^2(d\theta ^2 + \sin^2 {\theta} d\phi^2)\right]$$ (1.2)

where $\{r, \theta, \phi\}$ to the physical distance objects. The parameter K can take the three values (-1,0,1) which correspond to three types of homogeneous and isotropic universes distinct: opened, flat or closed. These geometries correspond respectively, in the case of a universe without cosmological constant, with expanding universes: infinite, asymptotic and finished. H. P. Robertson and A.G. Walker introduced this metric which bear their names.

One often expresses $l(t) = l_0 a(t)$.

If the following co-ordinates are introduced:

$$d\chi =\frac{dr}{\sqrt{1-kr^2}}$$

maybe,

$$r=S_k(\chi)$$

with

$$\left \{ \begin{array}{lll} S_{-1}(\chi) & = & \sin{\chi}\\ S_{0}(\chi) & = & \chi\\ S_{1}(\chi) & = & \rm {\cosh} {\chi} \end{array} \right.$$

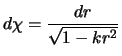
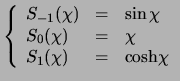
then one can rewrite the metric one in the form:

$$ds^2 = dt^2 -R ^2(t)\left[d\chi^2 + S_k^2(d\theta^2 + \sin^2\theta d\phi^2) \right]$$ (1.3)

In this frame of reference, an object whose co-ordinates $\{\chi, \theta, \phi\}$ remain constant in the course of time is motionless, made abstraction of the general expansion of the universe which is included/understood in the factor $dl = R(t) d\chi$.

The most remarkable property of this metric is that it introduces naturally, through the scale factor, the dynamics of the universe. The universe can be expanding or contraction.