$\star$ Diagram of Hubble and relations of standardization

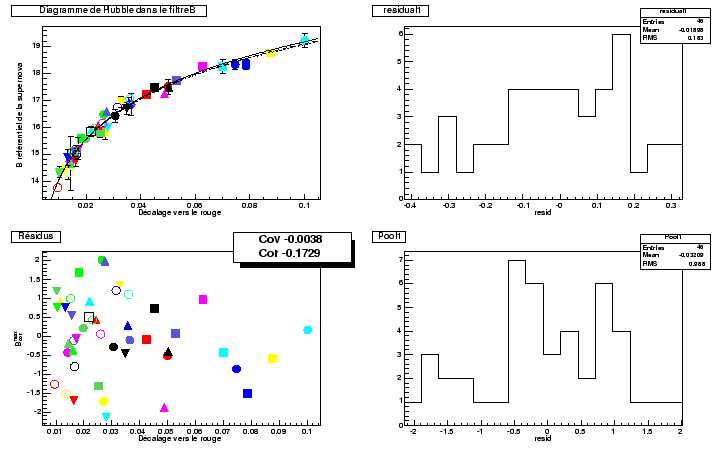
Figure 10.9 shows the diagram of Hubble obtained by adjusting the parameters of standardization $\beta$. We find a dispersion 0.18 magnitude comparable with the dispersions observed for the other analyses (perlmutter1999 & riess1998).

Figure 10.9: Diagram of Hubble out of B corrected for the factor of stretching and the color. In top, on the left, the Diagram of Hubble. In bottom, on the left residuals with the diagram of Hubble in a number of $\sigma$ according to the redshift. In top on the right, the histogram of the residuals in magnitude, bellow on the right, the sweater of the residuals.

We find finally the relation of following standardization:

$$m_B(z) - 24.02~(0.07) = \mu(z,\Omega_{\rm M},\Omega_\Lambda ) + 0.78~(0.47) \times (1-s_B) + 3.04 ~(0.36) \times{(B-V)_{MAX}}$$ (10.5)

The principal source of uncertainty comes from the contribution of the error on the color and the significant value of the parameter $\beta$.