The model of lightcurve

We can thus write for an effective filter $T_{eff}(\lambda)$ and a shift towards red Z:

$$f(t) = \frac{1}{d_L^2(z) 4\pi} ~ \int_{\lambda_{obs}} SN(t_{obs}/(1+z),\lambda_{obs}/(1+z)) ~ T_{eff} ~(\lambda) S_{miroir} d\lambda$$ (9.3)

where $d_L(z)$ the distance from luminosity given by equation 9.4 shows a simulation of lightcurve of a supernova to a redshift of 0.5.

Appear: Curves of light simulated in the filters R and I of instrument WFPC2 of the Hubble telescope for a supernova with a redshift of 0.5.

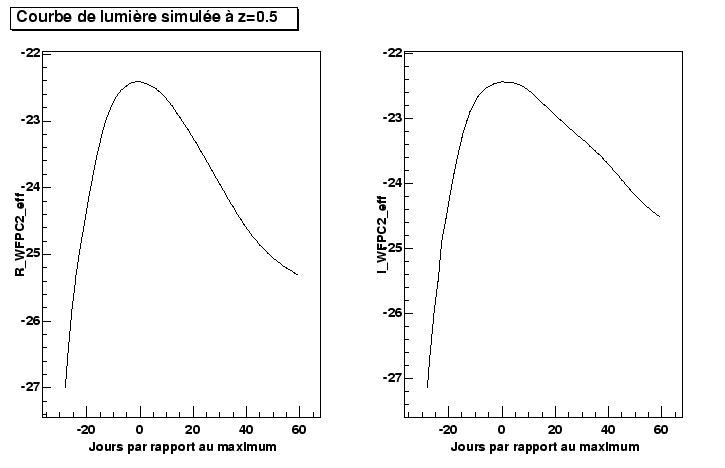This simulator of lightcurve will enable us to adjust the parameters of our lightcurves. Let us see finally how we take account of the absorption of the light by the clouds of dust in our galaxy.