$\star$ Points zero synthetic

To reproduce synthetic zero points, in addition to the effective filters, we must know the collecting surface of the mirror $S_{miroir}$. This term is in general relatively badly known, however, it does not depend on the wavelength. We thus used an approximate surface of mirror, it is the comparison with the zero points observed which enabled us to standardize the effective filters correctly.

If the effective filters are correct standardization should be similar for all the filters.

By considering zero points in the standard system and by using the spectrum of Vega $\epsilon$, we have:

$$zero_{filtre} = 2.5 \log_{10} \left(\int_\lambda T_{eff}(\lambda) ~\epsilon ~S_{miroir} ~V(\lambda) d\lambda \right)$$ (9.2)

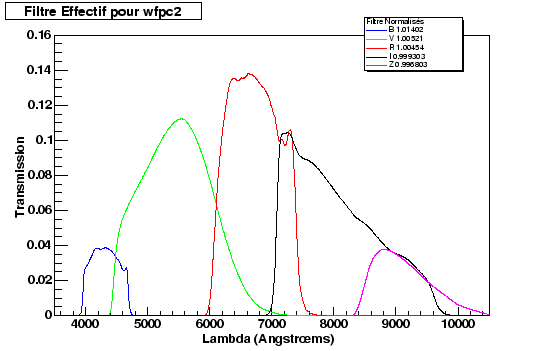
Figure 9.2 shows the effective filters built starting from the filters provided by STsCI. The size of the mirror was adjusted so as to reproduce items zeros observed. We see on figure 9.2 that the standardization from one filter to another is almost constant indicating that the filters were correctly evaluated.

Figure 9.2: Effective filters BVRIZ of instrument WFPC2 of the Hubble telescope standardized to reproduce zero points observed. Standardization is close to 1 and varies only very little from one filter to another.