$\star$ Alignment of the PSF and estimate of the position

The estimate of the position is of primary importance in the estimate of flux. The influence is tiny if one considers a photometry of opening of large ray. On the other hand, it becomes crucial when photometry of PSF is made.

Indeed, a bad estimate of the position will give more weight to pixels of less flux and a more significant weight with pixels of less flux giving an estimate biased to the bottom of the flux of the object considered.

The method employed here is an estimate of the position of the object by calculating a weighed barycentre of the image:

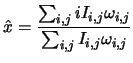$$\hat x = \frac{\sum_{i,j} i I_{i,j} \omega_{i,j} }{\sum_{i,j}I_{i,j}\omega_{i,j}}$$ (8.14)

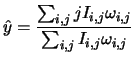$$\hat y = \frac{\sum_{i,j} j I_{i,j} \omega_{i,j} }{\sum_{i,j}I_{i,j}\omega_{i,j}}$$ (8.15)

Where $\omega_{i, j}$ the weight of the pixel.

The optimal weight for the estimate of the positions is given by Irwin1985. It depends on the flux of the object and on derived from the PSF compared to the co-ordinate considered. At first approximation, the profile of stars is Gaussian, the PSF is thus a good approximation of its derivative.

In this approximation, the weight $\omega_{i, j}$ is written:

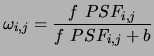$$\omega_{i,j} = \frac{f~PSF_{i,j}}{f~PSF_{i,j} + b}$$ (8.16)

where $\hat y$, and that one thus has only one implicit definition of the estimator of position.

HuPhot uses this algorithm for the estimate of the positions, by using a barycentre like starting point. One can then suitably align the PSF discretized on the pixels of the image, evaluate the weights and estimate a new position. One reiterates this process until convergence.

In this process, the PSF is rééchantillonée and centered with each iteration on the estimated position. At the end of the process, we have an estimate of the positions as well as model of PSF aligned on star considered. This model will be used for the estimate of fluxes.