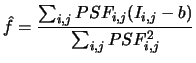Weighed photometry

So now, it is supposed that the variance of the flux of the object is negligible in front of the variance of the bottom of sky, the estimate of flux becomes:

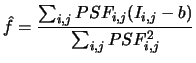$$\hat f = \frac{\sum_{i,j} PSF_{i,j}(I_{i,j} -b)}{\sum_{i,j}PSF_{i,j}^2}$$ (8.8)

The variance is written:

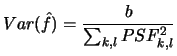$$Var(\hat f) = \frac{b} {\sum_{k,l} PSF_{k,l}^2}$$ (8.9)

This variance does not depend on flux; the average standard deviation increases like the square root of the bottom of sky, and like dimension characteristic of the PSF (i.e. the seeing).

For weak fluxes weighed photometry is a measurement of the flux of star on each pixel balanced by the flux awaited in this pixel. Let us note that no preliminary knowledge of F is necessary to evaluate the variance of each pixel. Here as, one must in practice limit integration to an opening on the object, without however as that has a crucial influence on the variance of $\hat f$.