The seeing

Separate for some very close giant stars, it is impossible to solve stars spatially. One can thus make the approximation which them signal is specific. However, two effects combine to spread out this signal: diffraction by the optics of the telescope and turbulences of the atmosphere. For the observations on the ground, the effects due to the atmosphere are very largely dominant. The profile of a star is thus characterized by the impulse response of the system atmosphère/télescope, it is called in jargon PSF (for Point Spread Function, function of spreading out of a point source). We will abundantly use this term in the continuation of the talk. The seeing is defined like the width with middle height of this function of spreading out. The term of quality of image refers to the same concept.

The seeing is caused by turbulences on a small scale of the atmosphere in the troposphere and the bottom of stratosphere (at altitudes about ten kilometers). These turbulences are related to micro variations in temperatures (about the hundredth of degree) which vary the index of refraction of the air and involves distortions of the incidental plane waves. Micro the local variations of the direction of the luminous ray involves a random displacement of the image. The refraction depends on the density, the effect is thus more significant in the lowest layers of the atmosphere.

The seeing can be expressed in several units. That employee usually by the astronomers is the width with semi height (FWHM) of the radial profile of a star (Figure 7.11 ) expressed in seconds of arc. Under very good conditions of observations, this value can go down to 0.5 seconds from arc. The values usually observed in the good sites are between $1.2' '$. We use another expression of the seeing during the reduction: the standard deviation in units of pixels of the CCD. The relation between the two is:

$$seeing(FWHM) = 2\sqrt{2\ln{2}} ~ L_{pixel} ~ seeing(\sigma)$$ (7.17)

Where $L_{pixel}$ is the size of the pixel.

Figure 7.11: Radial profile of a star for an image taken with the CFHT. The ray is expressed in a number of pixel. The value of the seeing is for this image, the value of the width to semi height in pixel (three last values in yellow) multiplied by the size of the pixel (0.2 seconds of arc in the case of CCDs of the CFHT): $seeing(FWHM) = 4.29 \times 0.2 = 0.86' '$

The seeing is one of the factors (with the bottom of sky and absorption) which determine the quality of an image. Less is the seeing, larger east the quantity of signal on the central pixels of the sources. It is essential, as we will further see it, in the principal stages of the reduction: it must thus be measured in a precise and robust way.

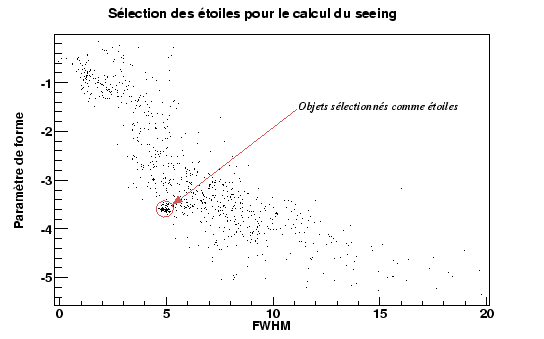
To determine the seeing it is necessary to build a star sample among the objects present in the image (galaxies, died, cosmic pixels).

With this intention, one uses the property which have the stars to have a width with middle height as well as a constant parameter of form. The parameter of form is defined here as the report/ratio bases of it logarithmic curve between the flux of the object and flux in the pixel highest of the object. As figure 7.12 shows it , there is an accumulation of objects for a particular value of the parameter of form and FWHM. These objects is selected for the calculation of the seeing, the average of the FWHM gives the value of the seeing.

However, this technique requires to have a significant number of objects (more than one hundred) and sufficiently good conditions (with a seeing smaller than $2' '$). In practice, these conditions are always carried out for the images which will be used to make detections.

Figure 7.12: Discriminations of stars in the plan parameter of form/width with middle height. The red circle indicates the position of the maximum in this diagram, it corresponds to stars. The determination of the maximum thus allows the calculation of the FWHM of stars, by definition: the seeing.