$\star$ Times of integration

Figure 7.4 gives the shift towards the limiting red according to the time of integration. To make this simulation, one considered a cosmology `` standard '' ( $\Omega_\Lambda = 0.72$) and filters it I of the CFH12K. The supernova is supposed to be with its maximum of luminosity. In this very favorable case, the CFH12K is able to detect with a cut in signal on noise of 5 of the supernovæ to the maximum until redshifts around 1.35 by considering exposures of 3h for the image of reference and research. It makes it possible to detect in a comfortable way (with a signal on noise around 10) of the supernovæ around 1.2 to the maximum, for conditions of average observations. That can seem comfortable, but insofar as the dates of the observations are forced enough, it is necessary to be able to face bad conditions of observation.

Figure 7.4: This figure presents the shift towards the limiting red obtained for the CFH12K in filter I according to the cut in signal on noise and for a duration 3 hours (for each image of reference and research). One considers the successful outcome where the supernova is with its maximum of light. Are considered three types of supernovæ, normals, under-luminous (0.1 less brilliant magnitude to the maximum) and on-luminous (0.1 magnitudes to the maximum). This figure shows that it is possible to discover a supernova with redshift of 1.2 with its maximum with a signal report/ratio on noise of 10 in 3h of integration.

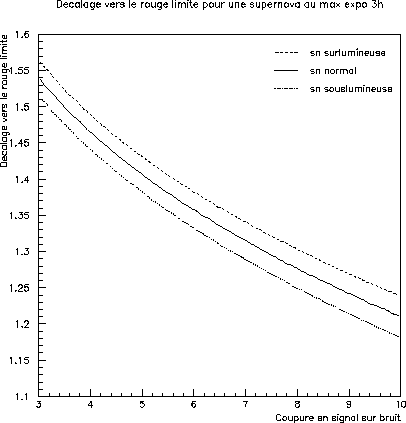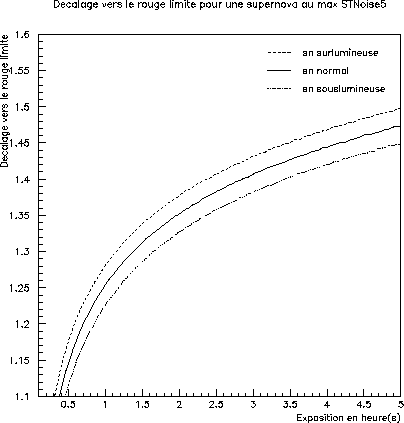
Figure 7.5 presents the shift towards the limiting red according to the duration. It is seen that the gain between 3h and 5h of exposure is tiny.

Figure 7.5: This figure presents the shift towards the limiting red according to the duration. For more precision to refer on figure 7.4 .

It was thus selected to carry out research with very great redshift by comparing images of 3h taken in filter I between 3 and 4 weeks of intervals. This duration corresponds to the boarding time of a supernova to a redshift of 0.5, that is to say $20\times (1+0.5) = 30$ days. What makes it possible in particular to detect the supernovæ before their maximum. Moreover, this duration makes it possible to carry out the observations around new moons, periods during which the light of the bottom of sky is the least significant.

Times of integration are such as it is impossible that the observations are carried out in only one installation. The first reason is that the sky saturates the CCD with the CFH12K with less than 40 mn to new moon. One is usually given for rule which the sky should not exceed a third of saturation. Moreover, as we will see it in the continuation, the cameras present a certain number of cosmetic defects (of the died columns, hot pixels...) which it is essential to label and to eliminate during the image processing. Is thus carried out to shifted split installations of a few seconds of arc between each installation . The typical time of installation out of I is 10 minutes for the CFH12K.

Moreover, split integration makes it possible to eliminate the artifacts present on only one installation like the cosmic rays. For a 10 minutes installation the number of cosmic rays on a CCD is indeed of the order of the thousand in Mauna Kea. Of the same one can thus detect the movement of the possible asteroids, same slow, present in the field, to eliminate them.