$\star$ Shift towards the limiting red

Knowing the limiting magnitude and by using equation 2.11 , it is possible to have an approximate expression of the shift towards the limiting red for an instrument.

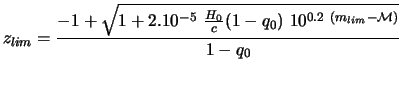$$z_{lim} = \frac{-1+ \sqrt{1 + 2.10^{-5} ~\frac{H_0}{c} (1-q_0) ~10^{0.2~(m_{lim}-{\cal M}) }}} {1-q_0}$$ (7.13)

However, this expression is valid only for shifts towards the small red in front of 1. Moreover, the value of ${ \cal M}_{filtre}$ (the value of intrinsic flux corresponds to the filter of observation) evolves with the shift to the red (see the K-corrections chapter 2.20 and to make a numerical integration.

In a very diagrammatic way, one can estimate that $\sqrt{D_m}T_p^{-1/4}$. The doubling of the time of integration makes it possible in practice to increase this shift towards the limiting red only of 20%.

It is thus primarily the size of the mirror which determines the depth of research.