The number of photons ![]() is written:
is written:
| (7.1) |
where ![]() is the flux of the supernova.
is the flux of the supernova.
The number of blows of ADC actually recorded by the camera depends on a
certain number of parameters like the gain of electronics of
acquisition, the quantum effectiveness of camera CCD, the transmission
of the filter and the transmission of optics. These various
contributions can have a strong dependence in wavelength (in particular
filters and to a lesser extent quantum effectiveness). For the moment
we will neglect these effects of color, we will return there abundantly
thereafter. We thus consider here whom the transmission of the
instrument can be described by only one number ![]() that we will take equal to his average value in the filter considered . Lastly, one includes in this term the attenuation by the atmosphere.
that we will take equal to his average value in the filter considered . Lastly, one includes in this term the attenuation by the atmosphere.
One can thus write:
| (7.2) |
where ![]() is the average number of recorded electrons. The noise associated with
measurement is mainly Poissonnian. The nonPoissonnian noise of reading
or shot effect is generally negligible compared to the noise of photon
induced by the bottom of sky in the case of the filters à.large.bande
busy for the images which we consider ( i.e. with long
durations). The various contributions in our case are the flux of the
supernova, the flux of the subjacent galaxy and the flux of the night
bottom of sky .
is the average number of recorded electrons. The noise associated with
measurement is mainly Poissonnian. The nonPoissonnian noise of reading
or shot effect is generally negligible compared to the noise of photon
induced by the bottom of sky in the case of the filters à.large.bande
busy for the images which we consider ( i.e. with long
durations). The various contributions in our case are the flux of the
supernova, the flux of the subjacent galaxy and the flux of the night
bottom of sky .
These various components not being correlated, one can write the variance of our flux like:
| (7.3) |
For major research, fluxes of the studied objects (supernova and galaxy host) are weak compared to fluxes of the bottom of sky, their contribution to the noise is thus negligible.
Finally, one can write the fluctuations of the flux of the supernova like:
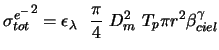 |
(7.4) |
One can thus express ![]() ) like:
) like:
| (7.5) |
One can finally write the signal report/ratio on noise like:
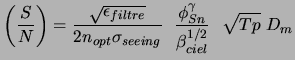 |
(7.6) |
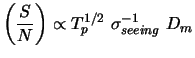 |
(7.7) |